Calcula el error muestral fácilmente con IBM SPSS: guía completa

En la realización de investigaciones y estudios estadísticos, es fundamental contar con medidas que nos permitan evaluar la precisión y fiabilidad de los resultados obtenidos. Uno de los conceptos más importantes en este sentido es el error muestral, que nos indica la variabilidad que existe entre los valores obtenidos en una muestra y los valores reales de la población en estudio. Calcular el error muestral de manera precisa y eficiente es esencial para obtener conclusiones confiables y tomar decisiones informadas.

Te presentaremos una guía completa sobre cómo calcular el error muestral utilizando IBM SPSS, uno de los programas más utilizados en análisis estadístico. Te explicaremos paso a paso el proceso para obtener esta medida, así como también te daremos algunos consejos y ejemplos prácticos para que puedas aplicarlo en tus propias investigaciones. ¡No te lo pierdas!

Qué es el error muestral y por qué es importante en la investigación

El error muestral es la diferencia entre el valor estimado de una población y el valor real. Es importante en la investigación porque nos permite evaluar la precisión de nuestros resultados y determinar qué tan representativos son de la población en general.

Al calcular el error muestral, podemos determinar la confiabilidad de nuestros hallazgos y tomar decisiones basadas en datos más sólidos. Además, nos ayuda a identificar posibles sesgos o errores en nuestra muestra, lo que nos permite ajustar nuestra metodología para obtener resultados más precisos.

Entender y calcular el error muestral es esencial para realizar investigaciones de alta calidad y tomar decisiones informadas basadas en datos confiables.

Cómo se calcula el error muestral utilizando IBM SPSS

El error muestral es una medida estadística que indica qué tan precisa es una estimación basada en una muestra en comparación con el valor real de la población. IBM SPSS es una herramienta muy útil para calcular este error de manera fácil y precisa.

Para calcular el error muestral con IBM SPSS, primero necesitamos tener los datos de la muestra. Una vez que tenemos los datos cargados en el software, podemos utilizar una variedad de métodos estadísticos para calcular el error muestral.

Método de la fórmula general

El método más común para calcular el error muestral es utilizando la fórmula general:

EM = Z (SD / √n)

Donde:
- EM es el error muestral
- Z es el valor crítico de la distribución normal estándar (por ejemplo, Z = 1.96 para un nivel de confianza del 95%)
- SD es la desviación estándar de la población
- n es el tamaño de la muestra

Utilizando IBM SPSS, podemos obtener estos valores fácilmente a través de funciones y comandos específicos. En el menú desplegable "Analyze", seleccionamos "Descriptive Statistics" y luego "Descriptives". Aquí podemos especificar las variables relevantes y obtener la desviación estándar.

Cuáles son las principales fuentes de error muestral y cómo se pueden minimizar

El error muestral es una preocupación común en la investigación estadística. Existen varias fuentes de error que pueden afectar la precisión de los resultados. La primera fuente de error es el error de muestreo, que ocurre cuando la muestra seleccionada no representa adecuadamente a la población objetivo. Para minimizar este error, es importante utilizar técnicas de muestreo aleatorias y estratificadas.

Otra fuente de error es el error de medición, que se produce cuando los instrumentos utilizados para recolectar datos introducen imprecisiones. Para minimizar este error, es esencial utilizar instrumentos de medición confiables y válidos, y capacitar adecuadamente a los encuestadores en su uso.

Además, el error de no respuesta es otro tipo de error muestral que se produce cuando los participantes seleccionados para la muestra eligen no participar o no responden completamente a las preguntas. Para minimizar este error, se pueden implementar estrategias como el uso de incentivos para aumentar la tasa de respuesta y el seguimiento activo de los no respondedores.

Finalmente, el error de procesamiento es otro factor a considerar. Este error se produce durante el procesamiento de los datos, como errores de codificación o entrada de datos incorrecta. Para minimizar este error, se pueden establecer procedimientos de control de calidad, como la verificación cruzada de datos o la utilización de software especializado en la gestión de datos.

El error muestral puede provenir de diferentes fuentes, pero existen estrategias para minimizarlo. Utilizando técnicas de muestreo adecuadas, instrumentos de medición confiables, estrategias para aumentar la tasa de respuesta y procedimientos de control de calidad en el procesamiento de datos, se puede reducir la probabilidad de error y aumentar la precisión de los resultados.

Puedo confiar en los resultados de una muestra pequeña o es necesario tener una muestra grande para obtener resultados precisos

Esta es una pregunta común que muchos investigadores se hacen al analizar datos de muestra. La respuesta es que la precisión de los resultados de una muestra depende del tamaño de la muestra y del error muestral asociado. El error muestral es una medida de la precisión de una muestra y se calcula utilizando una fórmula estadística específica.

En general, se recomienda tener una muestra lo suficientemente grande para obtener resultados precisos. Una muestra grande reduce el error muestral y aumenta la confianza en los resultados. Sin embargo, esto no significa que los resultados de una muestra pequeña sean necesariamente incorrectos. En algunas situaciones, una muestra pequeña puede ser suficiente para obtener resultados confiables.

Cuando se trabaja con una muestra pequeña, es importante tener en cuenta que el error muestral será mayor en comparación con una muestra grande. Esto significa que los resultados pueden tener cierta variabilidad y no representar con precisión la población objetivo. Es por eso que es importante considerar el tamaño de la muestra y el error muestral al interpretar los resultados de una muestra pequeña.

Aunque una muestra grande ofrece resultados más precisos, es posible obtener resultados confiables incluso con una muestra pequeña. Sin embargo, es importante tener en cuenta el error muestral y la posible variabilidad asociada a una muestra pequeña al interpretar los resultados. En la próxima sección, exploraremos cómo calcular el error muestral utilizando IBM SPSS.

Cuál es la diferencia entre error muestral y error de muestreo

El error muestral y el error de muestreo son dos conceptos relacionados pero distintos en la estadística. El error muestral se refiere a la diferencia entre la estimación obtenida a partir de una muestra y el valor real de la población. Por otro lado, el error de muestreo se refiere a la variabilidad aleatoria que ocurre al seleccionar diferentes muestras de la población.

El error muestral es inevitable y puede ocurrir debido a varios factores, como la variabilidad intrínseca de la población, el tamaño de la muestra y el método de selección utilizado. Por lo tanto, cuando se realiza un estudio de investigación, es importante calcular el error muestral para obtener estimaciones precisas y confiables de la población.

Por otro lado, el error de muestreo se puede reducir mediante técnicas de muestreo adecuadas, como el muestreo aleatorio simple o el muestreo estratificado. Estas técnicas permiten minimizar el sesgo y la variabilidad en la selección de la muestra, lo que a su vez reduce el error de muestreo.

El error muestral es la diferencia entre la estimación de la muestra y el valor real de la población, mientras que el error de muestreo es la variabilidad aleatoria en la selección de muestras. Ambos conceptos son importantes de entender y calcular para obtener resultados confiables en estudios de investigación.

Cómo afecta el tamaño de la muestra al cálculo del error muestral

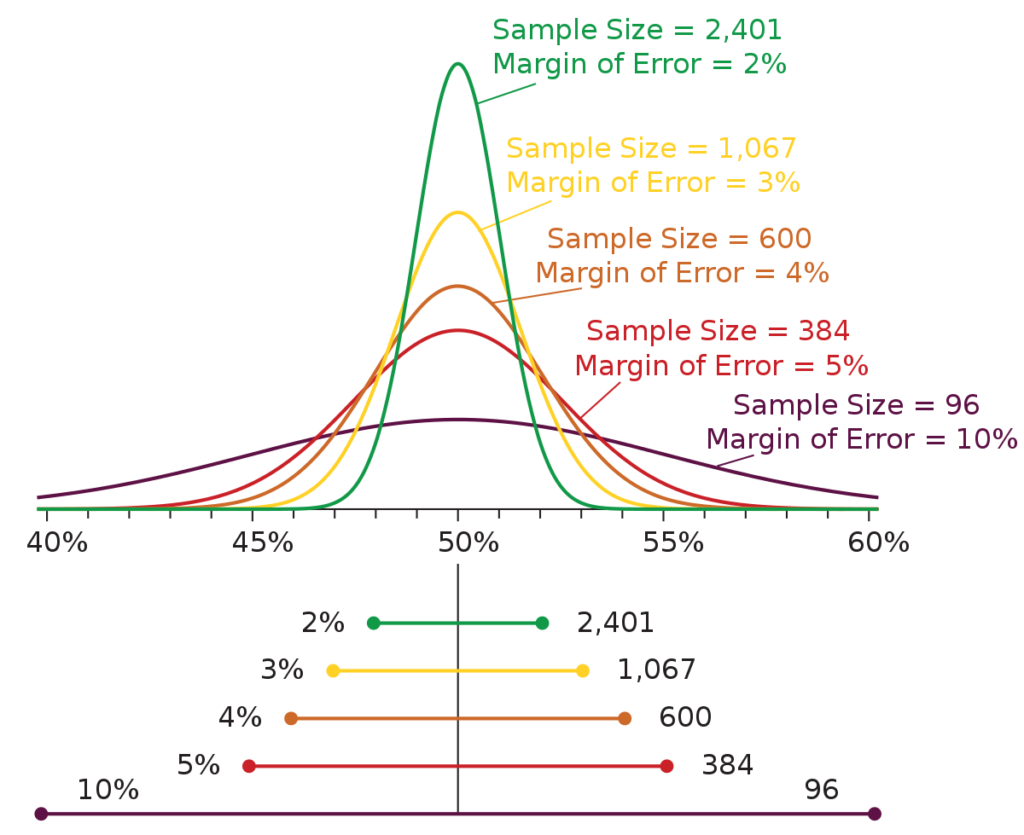
El tamaño de la muestra es un factor crucial en el cálculo del error muestral. A medida que aumenta el tamaño de la muestra, el error muestral tiende a disminuir. Esto se debe a que una muestra más grande proporciona una representación más precisa de la población total.

El cálculo del error muestral se basa en la fórmula E = Z (σ / √n), donde E es el error muestral, Z es el valor crítico, σ es la desviación estándar de la población y n es el tamaño de la muestra. A medida que n aumenta, el denominador √n disminuye, lo que resulta en un menor valor de E.

Por ejemplo, si se tiene una muestra de 100 individuos y se calcula el error muestral utilizando la fórmula mencionada, el resultado será mayor que si se utiliza una muestra de 1000 individuos. Esto se debe a que la raíz cuadrada de 1000 es mayor que la raíz cuadrada de 100, lo que hace que el denominador sea más pequeño.

Es importante tener en cuenta que el tamaño de la muestra óptimo varía según el tipo de estudio y los objetivos de investigación. En general, se recomienda utilizar una muestra lo suficientemente grande como para obtener resultados confiables, pero no tan grande como para hacer que el estudio sea costoso o difícil de administrar.

El tamaño de la muestra tiene un impacto significativo en el cálculo del error muestral. A medida que aumenta el tamaño de la muestra, el error muestral disminuye, lo que proporciona una estimación más precisa de la población total. Sin embargo, es importante encontrar un equilibrio entre el tamaño de la muestra y los recursos disponibles para el estudio.

Existen diferencias en el cálculo del error muestral para muestras aleatorias y no aleatorias

El cálculo del error muestral es esencial al realizar estudios de investigación, ya que nos permite estimar qué tan preciso es nuestro resultado en relación con la población de la que se obtuvo la muestra. Sin embargo, es importante tener en cuenta que existen diferencias en el cálculo del error muestral para muestras aleatorias y no aleatorias.

En el caso de las muestras aleatorias, el cálculo del error muestral se realiza mediante fórmulas estadísticas que tienen en cuenta tanto el tamaño de la muestra como la variabilidad de los datos. Estas fórmulas permiten obtener un margen de error con un nivel de confianza determinado.

Por otro lado, en el caso de las muestras no aleatorias, el cálculo del error muestral puede ser más complejo. En estos casos, es necesario tener en cuenta factores adicionales, como el sesgo de selección y la representatividad de la muestra. Además, es importante aplicar técnicas estadísticas adecuadas para estimar el margen de error de forma precisa.

Tanto en muestras aleatorias como no aleatorias, el cálculo del error muestral es fundamental para obtener resultados confiables en nuestros estudios. Es importante tener en cuenta las diferencias entre ambos tipos de muestras y aplicar las técnicas estadísticas adecuadas en cada caso.

Puedo utilizar el error muestral para medir la precisión de una encuesta o experimento

El error muestral es una medida de la precisión de una encuesta o experimento. Nos permite evaluar qué tan cerca está la muestra seleccionada del valor real de una población. Es importante comprender y calcular el error muestral para obtener resultados confiables y representativos.

Para calcular el error muestral, es necesario conocer el tamaño de la muestra y el nivel de confianza deseado. El tamaño de la muestra determina la precisión, mientras que el nivel de confianza se refiere a la probabilidad de que los resultados de la muestra sean representativos de la población en general.

IBM SPSS es una herramienta potente para el análisis de datos y cálculo del error muestral. Con SPSS, puedes realizar análisis estadísticos y calcular el error muestral de manera fácil y precisa.

Cómo calcular el error muestral utilizando IBM SPSS

El primer paso para calcular el error muestral con IBM SPSS es ingresar los datos de tu muestra en el programa. Puedes hacerlo manualmente o importar los datos desde un archivo externo. Una vez que los datos estén cargados, puedes comenzar a realizar los cálculos.

En IBM SPSS, el cálculo del error muestral se puede realizar utilizando diferentes técnicas, como el cálculo del margen de error o la estimación por intervalo de confianza. Estas técnicas te permiten obtener una medida precisa del error muestral y evaluar la confiabilidad de tus resultados.

Para calcular el margen de error en IBM SPSS, debes seleccionar la opción correspondiente en el menú de análisis. Luego, ingresarás el tamaño de la muestra y el nivel de confianza deseado. El programa realizará los cálculos necesarios y te mostrará el resultado del margen de error.

Si prefieres utilizar la estimación por intervalo de confianza, IBM SPSS también ofrece esta opción. Debes seleccionar la técnica de intervalo de confianza y especificar el nivel de confianza deseado. El programa realizará los cálculos y te mostrará el intervalo de confianza junto con el error muestral asociado.

El cálculo del error muestral utilizando IBM SPSS es una tarea sencilla y precisa. Esta herramienta te brinda las opciones necesarias para calcular el error muestral utilizando diferentes técnicas y obtener resultados confiables en tus análisis de datos.

Qué técnicas se pueden utilizar para reducir el error muestral en estudios de investigación

Reducir el error muestral en estudios de investigación es fundamental para obtener resultados más precisos y confiables. Afortunadamente, existen diversas técnicas que pueden ayudar a lograr este objetivo.

Una de las técnicas más comunes es aumentar el tamaño de la muestra. Cuanto mayor sea el tamaño de la muestra, menor será el error muestral, ya que se considera que la muestra es más representativa de la población total. Esto se debe a que un tamaño de muestra más grande permite capturar una mayor variedad de características y variaciones presentes en la población.

Otra técnica para reducir el error muestral es utilizar técnicas de muestreo estratificado. En lugar de seleccionar aleatoriamente a los participantes, se divide a la población en subgrupos o estratos y se selecciona una muestra representativa de cada estrato. Esto garantiza que cada estrato esté adecuadamente representado en la muestra, lo que reduce el sesgo y el error muestral.

Además, es importante tener en cuenta los métodos de muestreo utilizados. Un muestreo aleatorio simple es el método más básico y consiste en seleccionar aleatoriamente a los participantes de la población. Sin embargo, existen otros métodos de muestreo más complejos y eficientes, como el muestreo por conglomerados o el muestreo sistemático, que pueden ayudar a reducir el error muestral al aumentar la representatividad de la muestra seleccionada.

Por último, es crucial tener en cuenta la calidad de los datos recolectados. Si los datos tienen errores o están mal registrados, esto puede contribuir a un mayor error muestral. Por lo tanto, es importante realizar una validación de los datos y asegurarse de que sean precisos y confiables antes de realizar cualquier análisis. Esto puede implicar revisar manualmente los datos, eliminar valores atípicos o utilizar técnicas estadísticas para detectar errores o inconsistencias.

Reducir el error muestral en estudios de investigación es esencial para obtener resultados precisos y confiables. A través de técnicas como el aumento del tamaño de muestra, el uso de muestreo estratificado y la selección de métodos de muestreo adecuados, es posible minimizar el error muestral y mejorar la calidad de los datos recolectados. Además, la validación de los datos y la eliminación de posibles errores o inconsistencias son también pasos cruciales para garantizar la precisión de los resultados obtenidos.

Cuáles son las limitaciones del cálculo del error muestral utilizando IBM SPSS

El cálculo del error muestral utilizando IBM SPSS puede ser una herramienta útil para los investigadores, pero también tiene sus limitaciones.

Una de las limitaciones del cálculo del error muestral con IBM SPSS es que se basa en ciertas suposiciones, como la distribución normal de los datos y la independencia de las observaciones. Esto puede ser problemático si los datos no cumplen con estas suposiciones, lo que puede conducir a estimaciones inexactas del error muestral.

Otra limitación es que el cálculo del error muestral con IBM SPSS puede ser una tarea complicada, especialmente para aquellos que no tienen experiencia en estadísticas. Es importante comprender los diferentes métodos disponibles y cómo interpretar los resultados para evitar errores en los análisis.

Además, el cálculo del error muestral utilizando IBM SPSS no tiene en cuenta otros factores importantes, como el tamaño de la muestra y el diseño de muestreo utilizado. Estos factores pueden afectar la precisión y la representatividad de las estimaciones del error muestral.

Aunque el cálculo del error muestral con IBM SPSS puede ser una herramienta útil, es importante tener en cuenta sus limitaciones y considerar otras fuentes de error en el diseño y análisis de la muestra.

Cómo puedo interpretar los resultados del cálculo del error muestral

Interpretar los resultados del cálculo del error muestral es fundamental para comprender la precisión de los datos. El error muestral es una medida de la variación esperada entre una muestra y la población objetivo. En general, cuanto menor sea el error muestral, mayor será la precisión de los resultados obtenidos.

Para interpretar los resultados del cálculo del error muestral, es importante considerar su magnitud en relación al tamaño de la muestra. Un error muestral pequeño indica que los resultados son confiables y representativos de la población objetivo. Por el contrario, un error muestral grande implica que los resultados pueden estar sujetos a una mayor variabilidad y no ser tan representativos.

Es importante tener en cuenta que el cálculo del error muestral se basa en suposiciones estadísticas y no garantiza la precisión absoluta de los resultados. Otros factores, como la metodología de muestreo utilizada y la calidad de los datos recolectados, también pueden influir en la precisión de los resultados.

La interpretación de los resultados del cálculo del error muestral nos brinda una idea de la confiabilidad de los datos obtenidos a partir de una muestra. Un error muestral pequeño indica mayor precisión y confiabilidad, mientras que un error muestral grande sugiere una mayor variabilidad en los resultados. Es importante considerar el tamaño de la muestra y otros factores para una interpretación completa y precisa.

Qué recomendaciones se pueden seguir para obtener resultados más precisos al calcular el error muestral con IBM SPSS

Calcular el error muestral en IBM SPSS puede resultar complicado si no se siguen las recomendaciones adecuadas. A continuación, te presentamos algunos consejos para obtener resultados más precisos:

1. Tamaño de la muestra

Es importante asegurarse de que el tamaño de la muestra sea lo suficientemente grande para obtener resultados confiables. Un tamaño de muestra pequeño puede generar un error muestral mayor.

2. Selección aleatoria

La muestra debe seleccionarse de forma aleatoria para evitar sesgos en los resultados. Utiliza la función de selección aleatoria de IBM SPSS para garantizar la representatividad de la muestra.

3. Verificar supuestos

Antes de calcular el error muestral, verifica que los supuestos del análisis estén cumplidos. Esto incluye la normalidad de los datos, la independencia de las observaciones y la homogeneidad de las varianzas.

4. Utilizar fórmulas correctas

Asegúrate de utilizar las fórmulas correctas para calcular el error muestral. Consulta la documentación de IBM SPSS para conocer las fórmulas adecuadas según el tipo de análisis que estés realizando.

5. Realizar múltiples cálculos

Para aumentar la precisión de los resultados, realiza múltiples cálculos del error muestral y calcula la media de los resultados. Esto reducirá el margen de error y proporcionará una estimación más precisa.

6. Interpretar los resultados

Una vez calculado el error muestral, es importante interpretar correctamente los resultados. Considera el margen de error al analizar los resultados y ten en cuenta que este indica la variabilidad esperada en los resultados si se repitiera el estudio.

7. Consultar a expertos

Si aún tienes dudas sobre cómo calcular el error muestral con IBM SPSS, no dudes en consultar a expertos en estadística. Ellos podrán brindarte orientación y asesoramiento especializado.

Siguiendo estas recomendaciones, podrás obtener resultados más precisos al calcular el error muestral con IBM SPSS. Recuerda siempre verificar los supuestos y utilizar las fórmulas adecuadas para obtener estimaciones confiables.

Preguntas frecuentes (FAQ)

1. ¿Qué es el error muestral?

El error muestral es la diferencia entre la estimación obtenida de una muestra y el valor real en la población.

2. ¿Por qué es importante calcular el error muestral?

Calcular el error muestral nos permite tener una medida de qué tan confiables son los resultados obtenidos a partir de una muestra y nos ayuda a evaluar la precisión de nuestras estimaciones.

3. ¿Cómo se calcula el error muestral?

El error muestral se calcula dividiendo el error estándar de la muestra entre la raíz cuadrada del tamaño de la muestra.

4. ¿Qué es el error estándar de la muestra?

El error estándar de la muestra es una medida de la variabilidad de los valores en la muestra y nos indica cuánto puede variar la estimación en diferentes muestras obtenidas de la misma población.

5. ¿Cómo puedo calcular el error muestral utilizando IBM SPSS?

En IBM SPSS, puedes calcular el error muestral utilizando la función "Análisis de datos complejos" y seleccionando la opción de "Error estándar". Esto te dará el valor del error estándar de la muestra, que luego puedes utilizar para calcular el error muestral dividiéndolo entre la raíz cuadrada del tamaño de la muestra.