Calcula fácilmente la desviación típica en IBM SPSS Statistics 20

La desviación típica es una medida estadística que nos permite conocer cuánto se alejan los valores de un conjunto de datos con respecto a su media. Es una herramienta muy útil en el análisis de datos, ya que nos ayuda a comprender la dispersión de los valores y a identificar posibles patrones o tendencias.

Te mostraremos cómo calcular la desviación típica utilizando IBM SPSS Statistics 20, una potente herramienta de análisis estadístico. Te explicaremos paso a paso cómo ingresar tus datos, realizar el cálculo y obtener los resultados deseados. Además, te daremos algunos consejos útiles para interpretar correctamente los resultados obtenidos. ¡No te lo pierdas!

Qué es la desviación típica y por qué es importante en el análisis estadístico

La desviación típica es una medida estadística que muestra la dispersión de los datos con respecto a la media. Es importante en el análisis estadístico porque nos permite entender qué tan dispersos están los datos alrededor de la media. Cuanto mayor sea la desviación típica, mayor será la dispersión de los datos y viceversa.

Calcular la desviación típica es esencial para comprender la variabilidad de los datos y tomar decisiones informadas. Por ejemplo, si estamos analizando los resultados de un experimento científico, podemos utilizar la desviación típica para determinar qué tan confiables son los resultados y si existen diferencias significativas entre los grupos de estudio.

La desviación típica nos brinda información valiosa sobre la consistencia y variabilidad de los datos, lo que nos ayuda a comprender mejor el fenómeno que estamos estudiando y a tomar decisiones basadas en evidencia sólida.

Cuál es la fórmula para calcular la desviación típica

La desviación típica, también conocida como desviación estándar, es una medida estadística que mide la dispersión de un conjunto de datos. La fórmula para calcular la desviación típica es la siguiente:

desviacion_tipica = √

Donde:

• xi es el valor individual en el conjunto de datos
• media es la media aritmética del conjunto de datos
• Σ es la suma de los valores individuales
• n es el número total de elementos en el conjunto de datos

Utilizando esta fórmula, puedes calcular la desviación típica de cualquier conjunto de datos en IBM SPSS Statistics 20 de manera fácil y rápida.

Cómo se interpreta el valor de la desviación típica

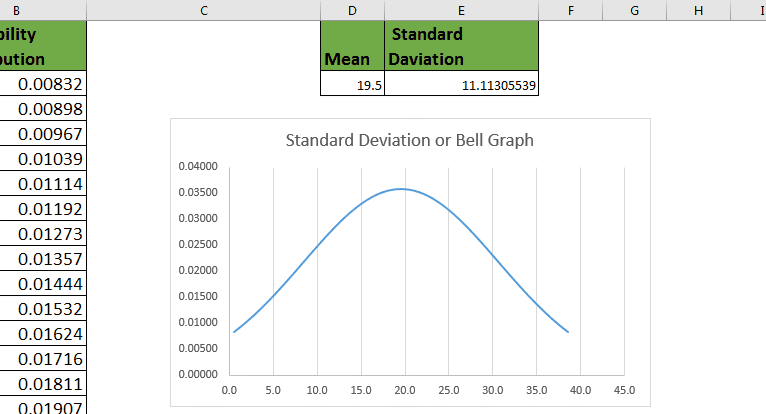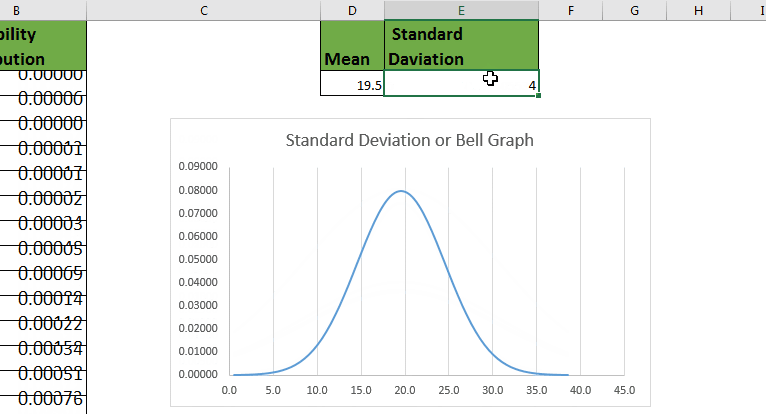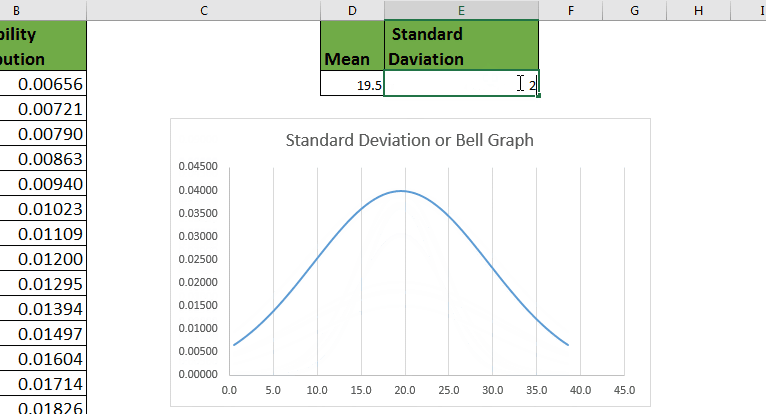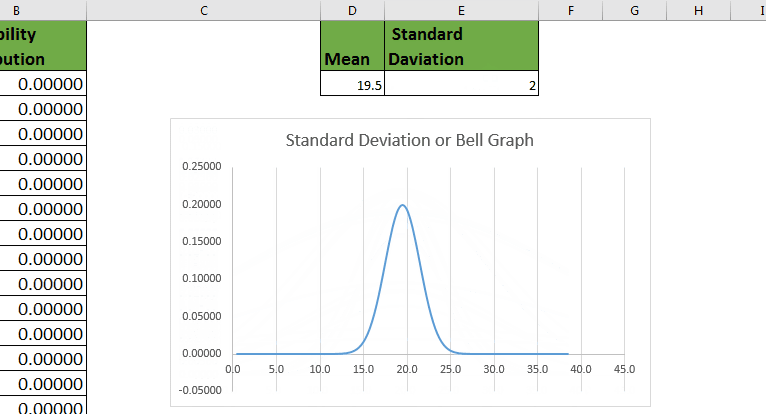
La desviación típica es una medida estadística que indica cuánto se alejan los datos de la media de una distribución. Un valor alto de desviación típica indica que los datos están más dispersos y alejados de la media, mientras que un valor bajo indica que los datos están más agrupados alrededor de la media.

Para interpretar el valor de la desviación típica, es útil compararlo con otros valores de la misma variable. Si el valor de desviación típica es mucho mayor o mucho menor que otros valores de la variable, puede indicar que hay datos atípicos o que la variable tiene una distribución no normal.

Es importante tener en cuenta que la desviación típica es sensible a los valores extremos, por lo que es posible que no sea una medida adecuada de la variabilidad si hay datos atípicos presentes en la muestra.

La desviación típica es una medida estadística que indica cuánto se alejan los datos de la media. Para interpretar su valor, es útil compararlo con otros valores de la misma variable y tener en cuenta la presencia de datos atípicos.

Cuál es la diferencia entre la desviación típica y la desviación estándar

La diferencia entre la desviación típica y la desviación estándar puede resultar confusa para muchas personas. Ambos conceptos se utilizan para medir la dispersión de un conjunto de datos, pero se calculan de manera ligeramente diferente.

La desviación típica es la raíz cuadrada de la varianza, que se obtiene sumando los cuadrados de las diferencias entre cada valor y la media, dividiendo luego esta suma por el número de valores y finalmente sacando la raíz cuadrada de ese resultado.

Por otro lado, la desviación estándar también se obtiene a partir de la varianza, pero en lugar de la raíz cuadrada, se calcula directamente. Esto significa que la desviación estándar es simplemente la raíz cuadrada de la varianza.

La desviación típica y la desviación estándar son medidas de dispersión relacionadas entre sí, pero con pequeñas diferencias en su cálculo.

Qué son los datos atípicos y cómo afectan a la desviación típica

Los datos atípicos, también conocidos como valores extremos, son valores que se encuentran muy alejados del resto de los datos en un conjunto. Estos valores pueden ser causados por errores de medición, errores de entrada de datos o por eventos raros o inusuales. Los datos atípicos pueden tener un impacto significativo en la desviación típica, ya que este estadístico se calcula teniendo en cuenta la distancia entre cada dato y la media. Si hay valores atípicos en el conjunto de datos, la desviación típica puede aumentar considerablemente, lo que indica una mayor dispersión de los datos.

Para identificar y tratar los datos atípicos, es importante realizar un análisis exploratorio de los datos y utilizar técnicas estadísticas adecuadas. Estas técnicas pueden incluir la eliminación de los valores atípicos, la transformación de los datos o el uso de métodos robustos que sean menos sensibles a la presencia de valores extremos. En SPSS Statistics 20, existen diversas herramientas y opciones disponibles que facilitan el cálculo y análisis de la desviación típica, permitiéndote identificar la presencia de datos atípicos y tomar las medidas necesarias para tratarlos adecuadamente.

Existen diferentes métodos para calcular la desviación típica en SPSS Statistics 20

El cálculo de la desviación típica es esencial para comprender la dispersión de los datos en un conjunto de datos. En SPSS Statistics 20, hay diferentes métodos disponibles para calcular la desviación típica. Uno de los métodos más utilizados es el cálculo manual, que implica realizar una serie de cálculos matemáticos paso a paso.

Para calcular la desviación típica manualmente en SPSS Statistics 20, primero debes calcular la media de los datos. Luego, debes restar cada valor individual de los datos de la media y elevarlo al cuadrado. Después, debes sumar todas las desviaciones al cuadrado y dividirlas por el número total de observaciones menos uno. Finalmente, debes calcular la raíz cuadrada del resultado para obtener la desviación típica.

Además del cálculo manual, SPSS Statistics 20 también ofrece la opción de calcular la desviación típica utilizando la función incorporada del software. Esta función automatiza el proceso y calcula la desviación estándar directamente a partir de los datos. Para utilizar esta función, simplemente debes seleccionar la columna de datos correspondiente y elegir la opción de calcular la desviación típica en el menú desplegable.

Es importante tener en cuenta que los resultados obtenidos pueden variar ligeramente dependiendo del método utilizado. Sin embargo, en la mayoría de los casos, los resultados serán similares y permitirán tener una idea clara de la dispersión de los datos en un conjunto de datos.

En SPSS Statistics 20, existen diferentes métodos para calcular la desviación típica. El cálculo manual implica una serie de pasos matemáticos, mientras que la función incorporada automatiza el proceso. Ambos métodos proporcionan resultados similares y son útiles para comprender la dispersión de los datos en un conjunto de datos.

Cómo se calcula la desviación típica en SPSS Statistics 20

La desviación típica es una medida estadística que nos permite conocer qué tan dispersos están los datos en relación a la media. En IBM SPSS Statistics 20, calcular la desviación típica es muy sencillo.

Para comenzar, abre el programa SPSS y carga el archivo de datos en el que deseas calcular la desviación típica. Asegúrate de tener la variable de interés seleccionada en la vista de datos.

A continuación, ve al menú "Analyze" y selecciona "Descriptive Statistics", y luego "Explore". En la ventana que aparece, arrastra la variable de interés al cuadro "Dependent List".

Luego, haz clic en el botón "Statistics" y marca la opción "Descriptives". Esto asegurará que SPSS calcule la desviación típica junto con otras estadísticas descriptivas, como la media y la mediana.

Finalmente, haz clic en "OK" y SPSS generará un informe con los resultados del análisis descriptivo, incluyendo la desviación típica de la variable seleccionada.

Recuerda que la desviación típica nos indica la dispersión de los datos alrededor de la media. Cuanto mayor sea la desviación típica, mayor será la dispersión de los datos. Por el contrario, cuanto menor sea la desviación típica, menor será la dispersión.

¡Con SPSS Statistics 20, calcular la desviación típica es rápido y sencillo, permitiéndote analizar la variabilidad de tus datos de manera eficiente!

Qué pasos debo seguir para realizar un análisis de desviación típica en SPSS Statistics 20

Para realizar un análisis de desviación típica en SPSS Statistics 20, debes seguir los siguientes pasos:

Paso 1: Abrir el archivo de datos

Lo primero que debes hacer es abrir el archivo de datos en SPSS Statistics 20. Puedes hacerlo yendo al menú "Archivo" y seleccionando "Abrir". Asegúrate de seleccionar el archivo correcto

Paso 2: Seleccionar la variable a analizar

Una vez que hayas abierto el archivo de datos, debes seleccionar la variable para la cual deseas calcular la desviación típica. Puedes hacer esto yendo al menú "Datos" y seleccionando "Seleccionar casos".

Paso 3: Calcular la desviación típica

Una vez que hayas seleccionado la variable, debes calcular la desviación típica. Para hacerlo, ve al menú "Analizar" y selecciona "Estadísticos descriptivos". Asegúrate de marcar la opción "Desviación típica" y haz clic en "Aceptar".

Paso 4: Obtener los resultados

Por último, debes obtener los resultados del análisis de desviación típica. Estos resultados se mostrarán en la ventana de salida de SPSS Statistics 20. Puedes acceder a la ventana de salida y ver los resultados haciendo clic en la pestaña "Salida".

¡Y eso es todo! Siguiendo estos simples pasos, podrás calcular fácilmente la desviación típica en SPSS Statistics 20.

Cuáles son las limitaciones o consideraciones importantes al interpretar la desviación típica en SPSS Statistics 20

La desviación típica es una medida estadística que nos permite conocer la dispersión de los datos con respecto a la media. En SPSS Statistics 20, esta medida se calcula de forma automática al realizar análisis de datos. Sin embargo, es importante tener en cuenta algunas limitaciones y consideraciones al interpretar los resultados.

En primer lugar, la desviación típica es una medida sensible a los valores extremos o atípicos en los datos. Si tenemos valores muy alejados de la media, esto puede incrementar considerablemente la desviación típica y distorsionar la interpretación de la variabilidad real de los datos.

Por otro lado, la desviación típica solo nos da una idea general de la dispersión de los datos, pero no nos indica la forma en que están distribuidos. Es decir, dos conjuntos de datos pueden tener la misma desviación típica, pero tener distribuciones completamente diferentes.

Además, es importante recordar que la desviación típica es calculada a partir de una muestra de datos, por lo que puede existir un margen de error asociado a la estimación de la desviación típica poblacional. Este margen de error puede variar dependiendo del tamaño de la muestra y la representatividad de los datos.

Al interpretar la desviación típica en SPSS Statistics 20, es importante tener en cuenta las limitaciones y consideraciones mencionadas. Es recomendable realizar un análisis más detallado de los datos, como la observación de gráficos y otras medidas estadísticas, para obtener una comprensión completa de la variabilidad de los datos.

Cuándo es recomendable utilizar la desviación típica en lugar de otros indicadores de dispersión en SPSS Statistics 20

La desviación típica es una medida de dispersión que indica cuánto se alejan los datos de una muestra o población de su media. En SPSS Statistics 20, es recomendable utilizar la desviación típica en lugar de otros indicadores de dispersión, como el rango o la desviación media absoluta, cuando se necesita conocer la variabilidad de los datos sin importar si hay valores extremos.

La desviación típica es especialmente útil cuando se trabaja con datos que siguen una distribución normal, ya que puede proporcionar una estimación precisa de la dispersión de los datos alrededor de la media. Además, se puede utilizar para comparar la variabilidad entre diferentes grupos o categorías en un análisis de datos.

En SPSS Statistics 20, calcular la desviación típica es sencillo. Simplemente selecciona la variable de interés y utiliza la función "Descriptives" para obtener un resumen de estadísticas descriptivas, que incluye la desviación típica. También puedes utilizar la función "Explore" para obtener un análisis más detallado de la desviación típica de una o varias variables.

La desviación típica en SPSS Statistics 20 es una herramienta poderosa para analizar la variabilidad de los datos. Su facilidad de uso y su capacidad para proporcionar una medida precisa de la dispersión la convierten en una opción recomendable en muchos casos.

Cómo puedo utilizar la desviación típica en SPSS Statistics 20 para identificar patrones o tendencias en mis datos

La desviación típica en SPSS Statistics 20 es una herramienta poderosa para analizar y comprender patrones y tendencias en los datos. Al calcular la desviación estándar, podemos determinar cuánto se alejan los datos de su valor promedio, lo que nos proporciona información sobre la dispersión de los datos y la variabilidad de la muestra.

Para utilizar la desviación típica en SPSS Statistics 20, sigue estos pasos:

Paso 1: Preparar los datos

Antes de poder calcular la desviación típica, es necesario importar los datos en SPSS Statistics 20. Asegúrate de que tus datos estén organizados en columnas y que cada columna represente una variable. De esta manera, podrás realizar análisis más precisos y detallados.

Paso 2: Calcular la desviación típica

Una vez que tus datos estén preparados, puedes calcular la desviación típica utilizando la función "Desviación estándar" de SPSS Statistics 20. Para hacerlo, ve a "Analyze" en la barra de menú y selecciona "Descriptives" y luego "Descriptives". En la ventana emergente, selecciona las variables para las cuales deseas calcular la desviación típica y haz clic en "OK". SPSS Statistics 20 generará entonces un informe que incluirá la desviación típica para cada variable seleccionada.

Paso 3: Interpretar los resultados

Una vez que hayas calculado la desviación típica, puedes interpretar los resultados para identificar patrones o tendencias en tus datos. Una desviación típica baja indica que los datos se encuentran cerca del promedio, mientras que una desviación típica alta indica que los datos están más dispersos o variados. Utiliza esta información para analizar tus datos y extraer conclusiones significativas.

La desviación típica en SPSS Statistics 20 es una herramienta esencial para analizar patrones y tendencias en los datos. Sigue estos pasos para calcular la desviación típica y utiliza los resultados para obtener información valiosa sobre la dispersión y variabilidad de tus datos.

Preguntas frecuentes (FAQ)

1. ¿Qué es la desviación típica?

La desviación típica es una medida que indica la dispersión de un conjunto de datos con respecto a su media.

2. ¿Para qué se utiliza la desviación típica?

La desviación típica se utiliza para determinar qué tan dispersos están los datos con respecto a su media y para comparar la variabilidad entre diferentes conjuntos de datos.

3. ¿Cómo se calcula la desviación típica en IBM SPSS Statistics 20?

En IBM SPSS Statistics 20, la desviación típica se calcula utilizando la función DESV para un conjunto de datos específico. Esta función devuelve el valor de la desviación típica de los datos.

4. ¿Qué indica una desviación típica alta?

Una desviación típica alta indica que los datos están más dispersos alrededor de la media, lo que significa que hay una mayor variabilidad en los datos.

5. ¿Qué indica una desviación típica baja?

Una desviación típica baja indica que los datos están más cercanos a la media, lo que significa que hay una menor variabilidad en los datos.